
Quantum optimization and machine learning
Quantum computers’ ability to manipulate whole probability distributions at once is very powerful for constrained optimization problems — problems where the number of countable solutions grows extremely rapidly with the size of the problem. They can also help with machine learning problems, making connections between inputs and “learning” how strong those connections should be. By looking at pairs of known inputs and outputs, quantum computers let researchers exploit a rich set of connections and therefore build more sophisticated and powerful models.
Optimization algorithms occur often in the analysis of high-energy physics data, such as fitting waveforms from particle detectors to templates to determine particle energies and finding the best set of candidate paths that are closest to a particle’s true trajectory. Fermilab is starting with determining quantum algorithms for solving very basic problems and then scaling them up to eventually be applicable to the kinds of problems that need to be solved in high-energy physics.
HEP applications
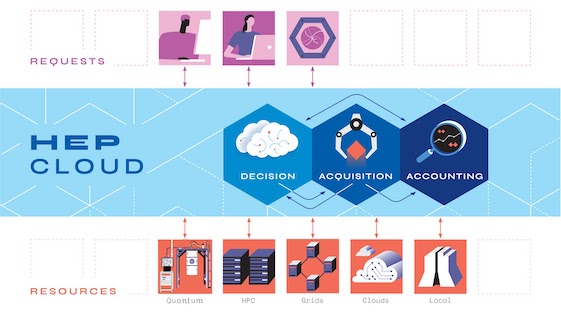
Fermilab researchers are looking into ways to use existing infrastructure to enable easy access to quantum machines. Fermilab plans to interface HEPCloud, a Fermilab system that manages heterogeneous computing resources, with quantum computers. This allows researchers to more easily submit and manage particle physics workflows using classical and quantum resources. The Fermilab computing community is working to cast particle physics problems in a way that will make quantum computing beneficial, describing physics systems so that they’re expressible in qubits. Simulations will allow physicists to refine how they formulate problems, such as those in quantum chromodynamics or in physics beyond the Standard Model, into a form usable through quantum computing.

Theory applications
At Fermilab we have a very strong effort on quantum theory and applications. Quantum theory is the key to understanding everything we are doing in the science and technology of quantum. Theorists are studying how to move the quantum science ahead and use quantum devices to solve difficult quantum problems that not even the most powerful supercomputers can solve.
The quantum computer is a good abstract model for capturing all information processing that nature allows, including those at the most fundamental level — subatomic particles and forces. Fermilab theorists aim to explore and further develop connections between quantum science and quantum field theories, or QFTs, which provide the foundation for particle physics studies. QFTs allow theorists to describe and compute phenomena in a vast range of scale, including examples from the theory of quantum electrodynamics, the effective field theories of the strong and weak interactions at low energies, the gauge theories of the Standard Model of particle physics, and possible extensions beyond the Standard Model. Scientists are also investigating approaches to reducing error in quantum simulation of QFTs using the techniques of effective field theories. Of particular interest is simulation of quantum chromodynamics, known as QCD. They aim to leverage Fermilab’s expertise in lattice QCD computations to inform and improve quantum simulation.
Quantum computation of fermion and boson systems
Fermilab scientists are developing a way to use quantum computers to simulate some of the most basic interactions that hold our universe together. The particles that do this fall into two basic groups: fermions, which are the building blocks of matter, and bosons, which are field particles that pull on particles of matter. Scientists have already made strides in modeling systems made of fermions using quantum algorithms. It’s been more difficult to achieve this for boson systems. Scientists at Fermilab have found a way to model boson systems on quantum computers and are working on developing the model further. They are representing the boson system as a system of harmonic oscillators. Harmonic oscillation occurs everywhere in nature: the motion of a spring bobbing up and down, the vibration of a plucked string. These systems are well-understood and can be modeled precisely. In quantum mechanics, the harmonic oscillator motion is described by wave functions. Modeling boson systems as harmonic oscillators opens a door to achieving realistic simulations of the subatomic realm, simulations that include fermions and bosons alike.
Large-scale simulations of quantum systems on high-performance computing

The large-scale simulation of quantum computers shares many similarities with simulations in high-energy physics: Both must manage a vast array of variables. Both organize their inputs and outputs similarly. And in both cases, the simulations have to be analyzed and consolidated into results. Fermilab scientists, in collaboration with scientists at Argonne National Laboratory, are using high-energy physics tools to produce and analyze simulations using high-performance computers at the Argonne Leadership Computing Facility. They are simulating the operation of a qubit device that uses superconducting cavities from particle accelerators to maintain quantum information over a relatively long time. Their results will determine the device’s impact on high-energy physics algorithms using an Argonne-developed quantum simulator.

